Conditional Probability and the Monty Hall Game
In the poker-playing, black-jack stats movie 21, there’s a scene where the protagonist is in a lecture hall with the professor. They discuss a game-show where a contestant chooses one of three closed doors, two of which have a goat behind them and one of which has a car.
Monty, who knows where the car is, then opens one of the two remaining doors. The door he opens always has a goat behind it (he never reveals the car!). If he has a choice, then he picks a door at random with equal probabilities.

Monty then offers the contestant the option of switching to the other unopened door. If the contestant’s goal is to get the car, should she switch doors?
The protagonist in 21 nails the numbers behind the right answer, and throws in some pseudo-math jargon along the way. In a grand monologue, he disregards his intuition in favor of math and statistics.
Neither really helped me understand the correct answer. I had to see it to believe it.
The simulation from the Harvard Intro to Stats course did the job really well, and I went ahead and built my own in React.
Pick a door
Play the game here or simulate below.
| Switched | Stayed | |
| Attempts | 0 | 0 |
| Goats | 0 | 0 |
| Cars | 0 | 0 |
| Won % | 0.0 | 0.0 |
The Results
Play the game as many times as you want. As you play, look at the results table as it tracks your score. Take note. Which strategy seems to be working better for you? Switch or stay?
Now simulate the game with switch as many times as you want. I did 10,000. Do the same for stay .
- What do your results indicate?
- What win % does each of the strategies converge on?
- Can you reason why?
Giving Away the Answer
Wikipedia has a graphic that explains the results better than anything I’ve seen so far. I recommend reading the article first though.
Either way - here it is:
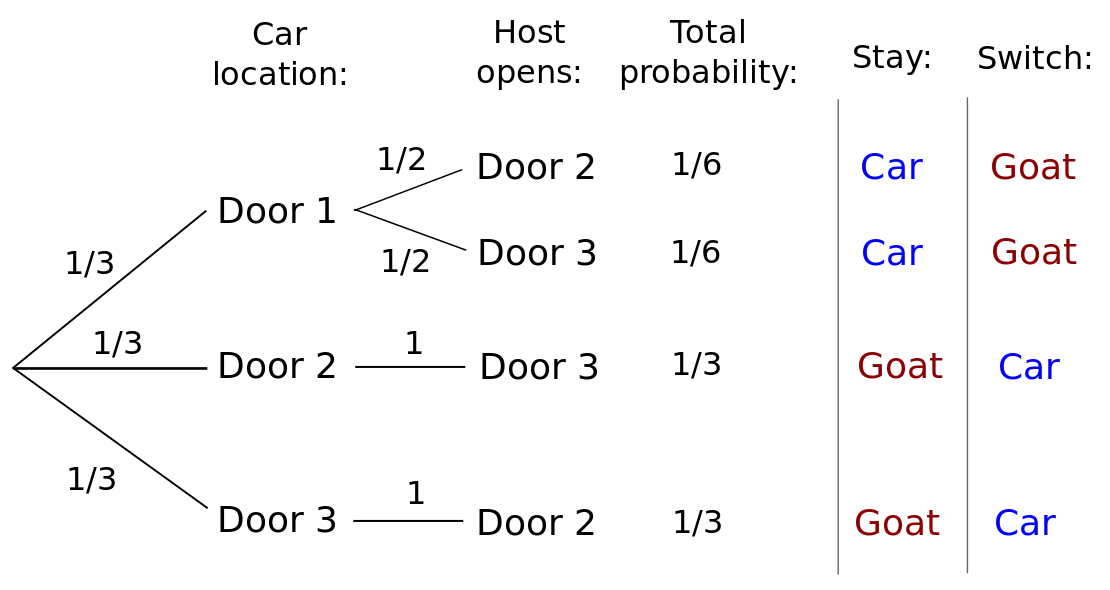
Does it make more sense now?
Tags:
Synthesized Statistics - Permutations and Combinations
Advent of Code - Day 2